GeometrieWerkstatt Gallery
Spacecurves

Elastic plane curves

Finite type curves in 2-dimensional spaceforms

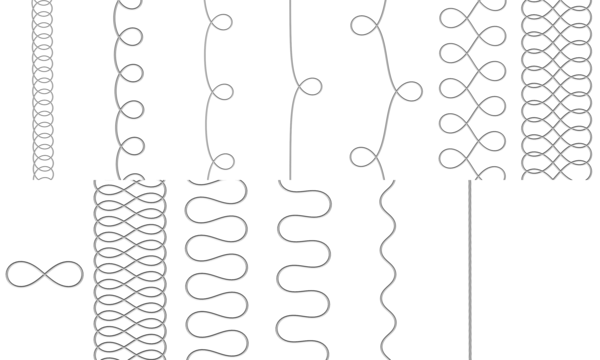
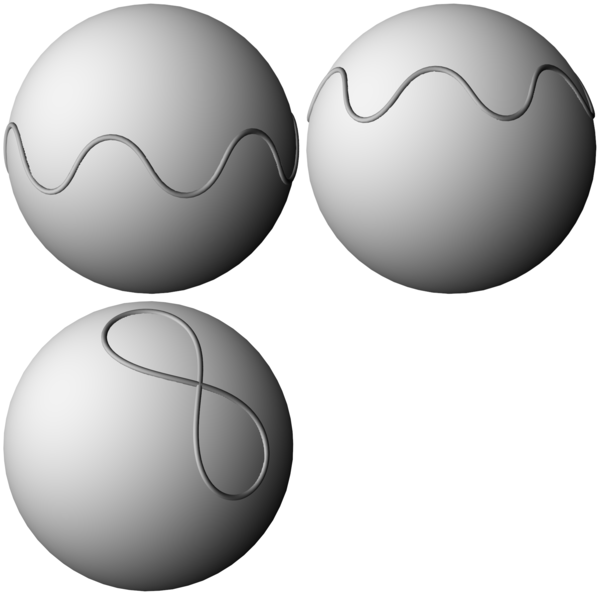
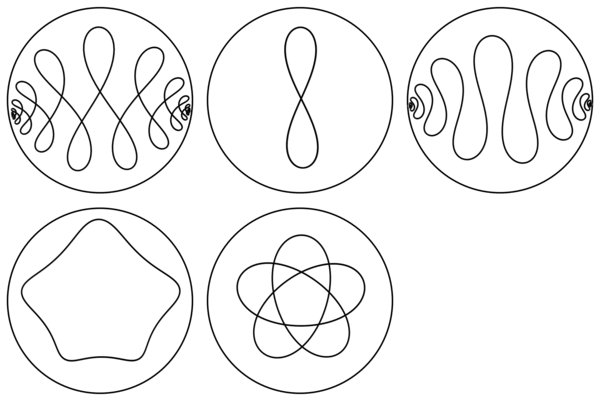
These curve minimize the total squared curvature. These curves were investigated by Euler in 1744 [2].

The first figure depicts the elastic plane curves in R2 of spectral genus 1 are shown in the first figure. The 1-looped example (fourth from left) with singular spectral curve demarcates the orbitlike (left) from the wavelike (right). The orbitlike starting at the singular example flow left, converging to a circle. The wavelike starting at the singular example flow right, passing through the closed Euler lemniscate, converging to a straight line.

The second figure depicts a sampling of closed finte type curves in S2 with low spectral genus. The elastic curve (first curve) with spectral genus 1 and six lobes, is symmetric about the equator. It can flow isoperiodically through constrained elastic curves with spectral genus 2 (second curve). The lemniscate (third curve) has spectral genus 1. These curves are profile curves of constrained Willmore Hopf tori [1,3].

The third figure depicts a sampling of elastic curves in H2 of spectral genus 1. The first three curve are wavelike. The last two closed orbitlike curves are related to profile curves of constant mean curvature tori of revolution [3,5].

The elastic plane curves in R2.
Closed finite type curves in S2 with low spectral genus.
Closed elastic curves in H2.

References

  1. C. Bohle, G. Peters, and U. Pinkall, Constrained Willmore surfaces, Calc. Var. Partial Differential Equations 32 (2008), no. 2, 263—277 [2389993].
  2. L. Euler, Methodus inveniendi lineas curvas maximi minimive proprietate gaudentes, sive solutio problematis isoperimetrici lattissimo sensu accepti, E065, eulerarchive.org (174).
  3. L. Heller, Constrained Willmore tori and elastic curves in 2-dimensional space forms, Comm. Anal. Geom. 22 (2014), no. 2, 343—369 [3210758].
  4. L. Heller, Constrained Willmore tori and elastic curves in 2-dimensional space forms, Comm. Anal. Geom. 22 (2014), no. 2, 343—369 [3210758].
  5. M. Kilian, M. Schmidt, and N. Schmitt, Flows of constant mean curvature tori in the 3-sphere: the equivariant case, arXiv:1011.2875, to appear in J. reine angew. Math., DOI 10.1515/crelle-2013-0079 (2010).