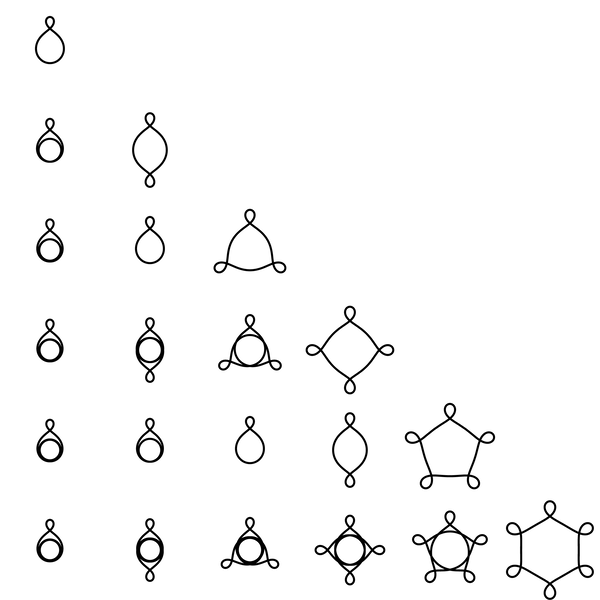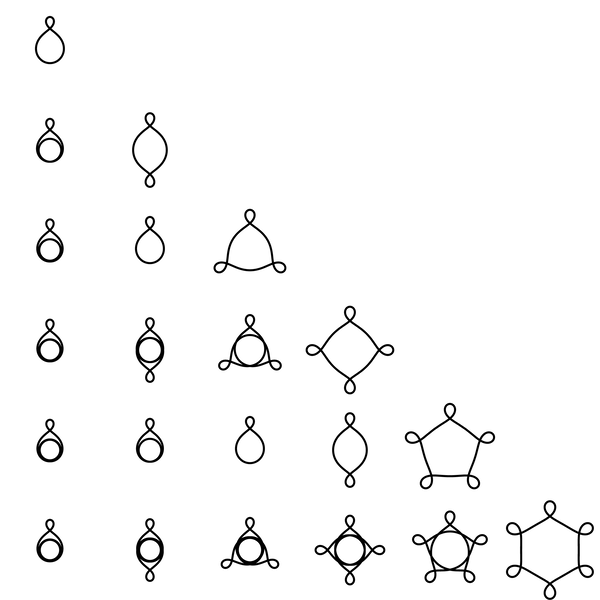

The first image depicts closed planar simple circletons (simple factor dressings of the circle) in R2. These curves are parametrized by pairs of positive integers (ℓ, w) satisfying ℓ < w, where ℓ is the lobe count and w is the wrapping number of the underlying circle. The image depicts circletons for small ℓ and w: the rows are indexed by w=2,…,7 and the columns by ℓ1,…,w-1
The second image depects the border line elastic curve, the unique (up to homothety) elastic planecurve in $\bbR^2$ with singular spectral curve. With arclength parametrization $(t-tanh 2t,sech 2t), it is a simple factor dressing of the vacuum (t,\,0). As indicated by the struts, the pointwise distance between the straight line and the Euler loop as arclength parametrized curves is constant 1.
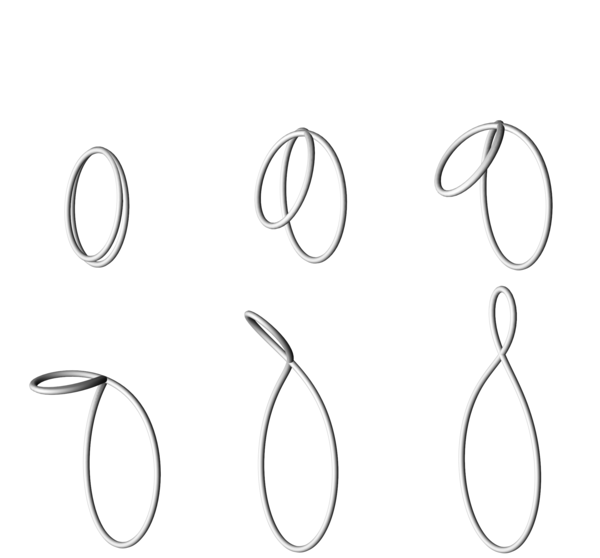
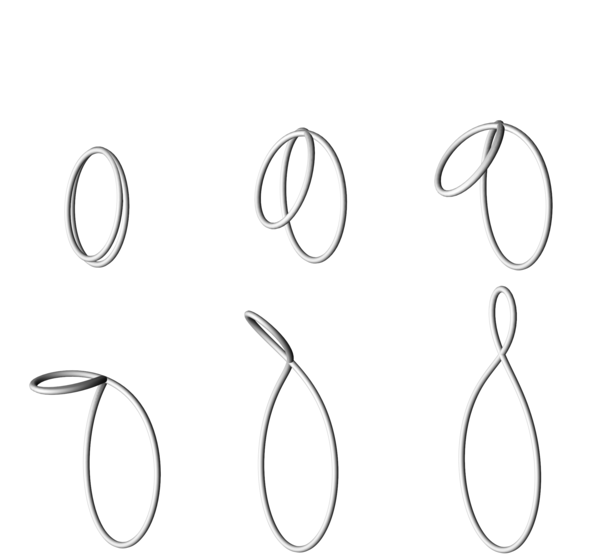
The third image depicts an isospectral flow through closed simple circletons (simple factor dressings of the circle) in R3. From right to left, the planar circleton (also appearing in the top row of the first figure) deforms to a 2-wrapped circle in the limit. The spectral curve for this family is singular with algebraic genus 2 and geometric genus 0.
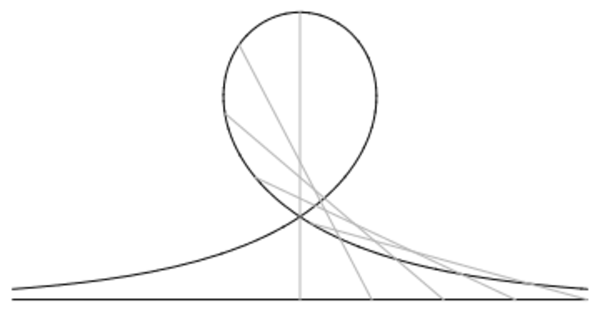
The fourth image depicts The Euler lemniscate (first curve), the unique closed elastic planecurve in R2 up to homothety; it is finite type with spectral genus 1. The image shows two views of the spacecurve in R3 constructed by dressing the Euler lemniscate by a simple factor, preserving closing Its spectral curve is singular.