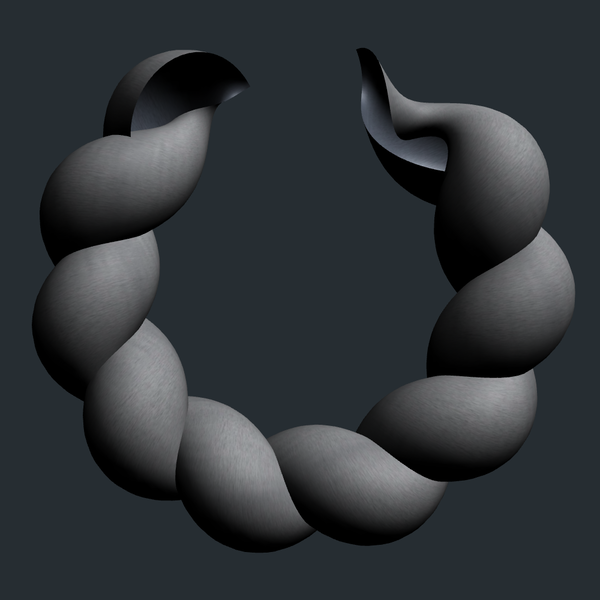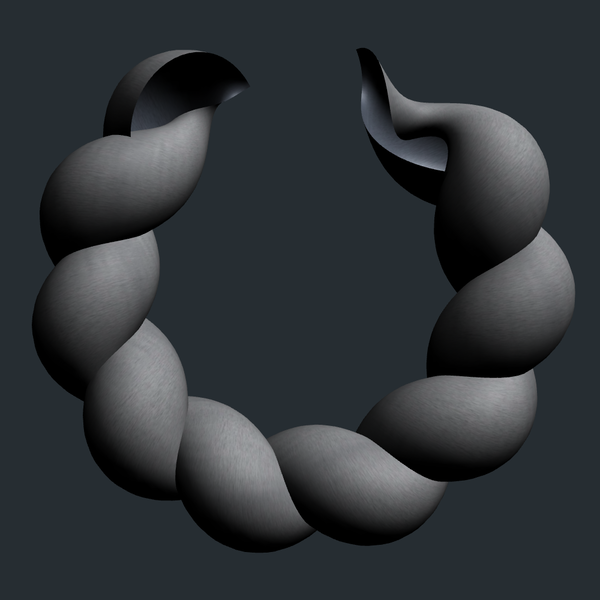
There is a flow through constant mean curvature (CMC) cylinders in euclidean 3-space with spectral genus 2 which reaches a dense subset of CMC tori along the way [2,1]. Starting at a twizzler (equivariant CMC surface) with a straight-line axis, and opening up a double point at the Sym point, the flow bends the straight axis into a circular “soul curve” with shrinking radius, leading to a Wente torus. The flow is as in [3] with closing conditions adapted to CMC cylinders in E3 [4].